4-DoF Robot – A Tutorial in MATLAB and Simulink

The forward kinematics problem is Calculating the matrix T₄

Select the base coordinate system and attach the coordinate systems to the links.

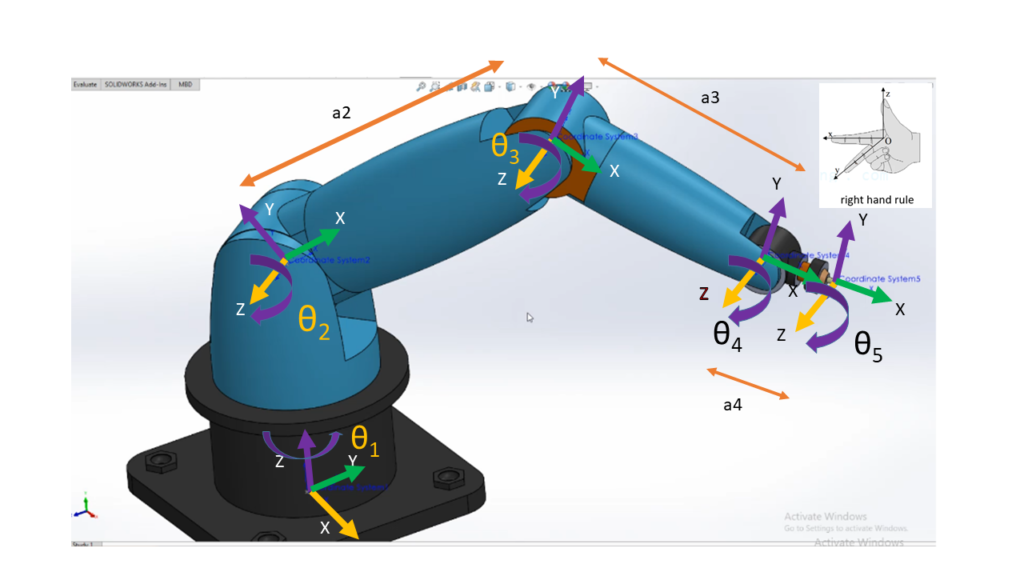
Kinematic parameter (Denavit – Hartenberg)

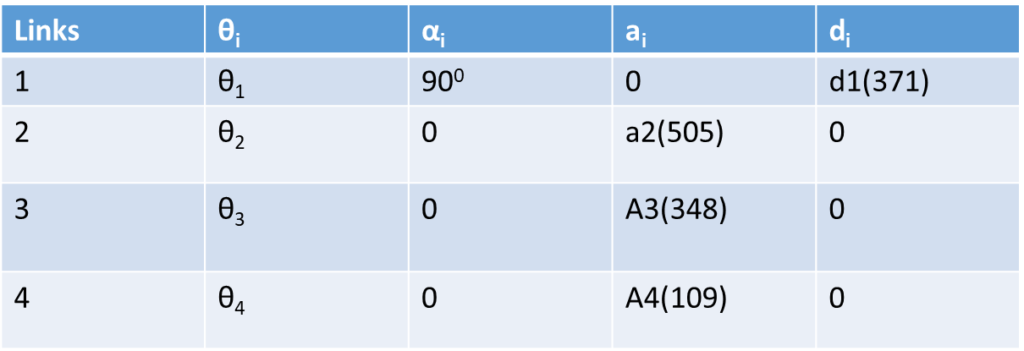
Θ_i :Angle of rotation about the Z axis

α : Angle of rotation of the Z axis around the X axis (positive counterclockwise)

a_i : Distance between axes Z

di:  Distance between axes Z

General Matrix

An=Rot(z,θ)Trans(0,0,d)Trans(a,0,0)Rot(x,α)

                      cosθ            -sinθcosα                sinθsinα             a cosθ

                       sinθ              cosθcosα             -cosθsinα            a sinθ

 A_n =               0                     sinα                       cosα                   d

                        0                       0                            0                       1

Using  Mat Lab  to calculate the Matrix T₄ 

T1 = [ C₁   0   – S₁      0;

           S₁    0 – C₁     0;

           0     -1   0   371;

           0     0     0       1];

T2 = [ C₂      – S₂    0     505*  C₂;

           S₂       0      C₂     505* S₂;

           0         0     1                0;

           0         0     0               1];

T3 = [ C₃   -S₃  0 348*C₃;

           S₃   C₃ 0  348*S₃;

           0     0   1           0;

           0     0   0          1];

T4 = [ C₄   -S₄  0 109*C₄;

           S₄   C₄    0 109*S₄;

            0     0     1           0;

            0     0     0         1];

T = T1*T2*T3*T4;

cos(θ₁) =C₁ ; cos(θ₂) =C₂ ; cos(θ₃) =C₃ ; cos(θ₄) =C₄ ;

sin(θ₁) =S₁; sin(θ₂) =S₂; sin(θ₃) =S₃; sin(θ₄) = S₄ .

INVERSE KINEMATIC Is calculating θ₁; θ₂;θ₃; θ4

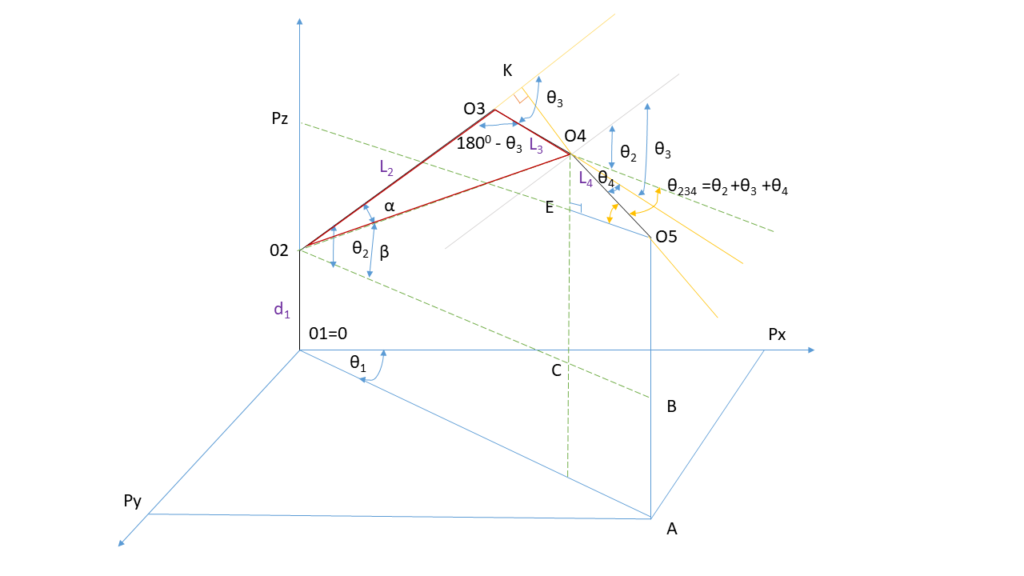
tan(θ₁ )= Py / Px  =>

θ₁ = atan2d(Py , Px)

Triangle O₂O₃O₄:

O₂O₄²= O₂O₃² +O₃O₄²   -2O₂O_3*O₃O₄  cos(180⁰ –θ₃ )       

cos(180⁰ –θ₃ )    =-cos(θ₃ )=    ((L₂ )² + (L₃ )² – O₂O₄ )/2*L₂L₃

Triangle O₂CO₄:

O₂O₄² =O₂C² + O₄C²

C234 = cos(θ₂₃₄)

S234 = sin(θ₂₃₄)

Triangle O₅EO₄:

O₄ E= L₄ *Sin(θ₂₃₄ )=L₄*S₂₃₄                                                                                                                 

O₅E=L₄ *Cos(θ₂₃₄ )=L_4*C₂₃₄

O₂C = O₂ B – BC = √(〖Py〗^2+〖Px〗^2 )   – L₄*C₂₃₄ 

O₄C = O₄ E + EC =  P_Z  – d1 + L₄*S₂₃₄ 

C₃=cos(θ₃)

C₃ =[( √(〖Py〗^2+〖Px〗^2 )   – L₄*C₂₃₄   )² + (P_z  – d1 + L₄*S₂₃₄ )²  – (L₂²   + L₃² ) ]/2*L2*L3   ;                  

S₃=√(1-〖C3〗^2 )

θ₃ = atan2d(S₃, C₃)